Re-use of this resource is governed by a Creative Commons Attribution-
Noncommercial-Share Alike 2.0 Licence UK: England & Wales
https://creativecommons.org/licenses/by-nc-sa/2.0/uk/
creative commons DoITPoMS logo

Ova animacija pokazuje nekoliko primena Fick-ovog drugog zakona. Izaberite scenario i kliknite "Continue" za dalje.


 



  



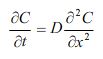
Intersticijska
primesa


Metal

Kod ovog slučaja konačnog izvora za difuziju, imamo intersticijsku primesu, koja se nalazi na levom kraju našeg komada metala. Pretpostavljamo da je širina zanemarljiva u poređenju sa metalom.

U ovoj situaciji, intersticijska primesa će difundovati kroz metal, dok sam metal neće uopšte difundovati

                   

Fick-ov drugi zakon
\[\frac{{\partial C}}{{\partial t}} = D\frac{{{\partial ^2}C}}{{\partial {x^2}}}\]
U ovom slučaju, granični uslovi za rešavanje Fick-ovog drugog zakona su:

\(C(x > 0,t = 0) = 0\) (Na početku, nema atoma primesa u metalu)

\(\int {C(x,t).dx = B} \)  (Ukupna kolličina atoma primesa ostaje konstantna)

gde je C(x,t) koncentracija primese. Rešenje za C je:

\[C(x,t) = \frac{B}{{\sqrt {\pi Dt} }}\exp \left( { - \frac{{{x^2}}}{{4Dt}}} \right)\]

Veličina D je
koeficijent difuzije atoma

                   

\[C(x,t) = \frac{B}{{\sqrt {\pi Dt} }}\exp \left( { - \frac{{{x^2}}}{{4Dt}}} \right)\]

D

t =
C x



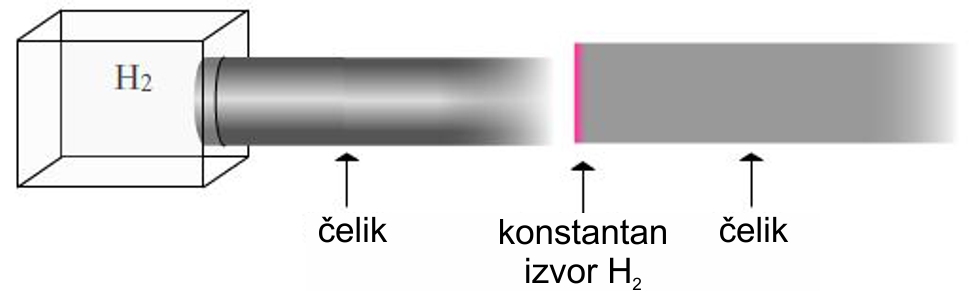
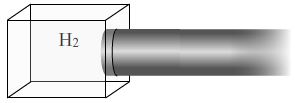
U ovom slučaju imamo H2 koji difunduje u čelik sa jedne strane. Pretpostavljamo da je čelični štap polubeskonačne dužine i da će koncentracija H2 ostati konstantna na granici čelika i H2. Nadalje ćemo difuziju prikazivati šematskim dijagramom (gornja desna slika)

U ovoj situaciji vodonik će difundovati u čelik, a čelični materijal neće uopšte difundovati

                   

Fick-ov drugi zakon
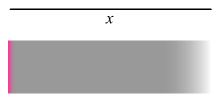
\[\frac{{\partial C}}{{\partial t}} = D\frac{{{\partial ^2}C}}{{\partial {x^2}}}\]

U ovom slučaju, granični uslovi za rešavanje Fick-ovog drugog zakon su:

\(C(x > 0,t = 0) = 0\) (Na početku, nema atoma primesa u metalu)

\(\int {C(x = 0,t) = B} \) (Koncentracija u x=0 je konstantna)

gde je C(x,t) koncentracija primese. Rešenje za C je:

\[C(x,t) = B - {\mathop{\rm e}\nolimits} rf\left( {\frac{x}{{2\sqrt {Dt} }}} \right)\]

Veličina D je koeficijent difuzije atoma
erf je (Gauss-ova) funkcija greške

                   

\[C(x,t) = B - {\mathop{\rm e}\nolimits} rf\left( {\frac{x}{{2\sqrt {Dt} }}} \right)\]

D

t =
C x



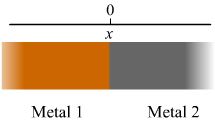
U ovom slučaju imamo dva polubeskonačna štapa jedan pored drugog. Pretpostavljamo da će se u oba metala pojaviti supstitucijska difuzija, pa će prvi metal difundovati u drugi, i obrnuto.
Takođe pretpostavljamo da oba metala imaju isti koeficijent difuzije.
Nadalje ćemo koristiti šematski dijagram za oba metala
(gornja desna slika)

                   

Fick-ov drugi zakon
\[\frac{{\partial C}}{{\partial t}} = D\frac{{{\partial ^2}C}}{{\partial {x^2}}}\]
Rešenje za ovaj problem je slično rešenju za konstantni izvor. Jedna velika razlika je u tome što je na granici koncentracija konstantna u B (50% metal 1, 50% metal 2).
To je zato što oba metala imaju isti koeficijent difuzije tako da je kod oba metala isti fluks kroz granicu. Kažemo da je koncentracija metala 1 100% u -∞, a koncentracija metala 2 je 100% u +∞
U našem rešenju, koncentracija metala 1, C1, će imati maksimalnu koncentraciju 100.
Onda će koncentracija metala 2 biti C2(x,t) = 100 - C1(x,t)
Rešenje je
\[C(x,t) = \frac{B}{{\sqrt {\pi Dt} }}\exp \left( { - \frac{{{x^2}}}{{4Dt}}} \right)\]
 
Veličina D je koeficijent difuzije atoma

                   

                   

\[C(x,t) = \frac{B}{{\sqrt {\pi Dt} }}\exp \left( { - \frac{{{x^2}}}{{4Dt}}} \right)\]
Metal 1     Metal 2

D

t =
C x